Een van de meest voorkomende vragen die aan een data-analist worden gesteld, is hoe de duur van klantrelaties, abonnementen of polissen correct kan worden bepaald. Marketeers hebben deze informatie nodig voor business cases om de waarde van klanten over hun hele levensduur te bepalen. Bovendien wordt de duur vaak gebruikt om cross-selling kansen, churn rates, en andere statistieken te analyseren. In de praktijk zien we vaak dat de duur eenvoudig wordt berekend door de einddatum af te trekken van de begindatum. Deze benadering kan echter leiden tot een vertekend beeld, omdat het geen rekening houdt met klanten, abonnementen of polissen die nog actief zijn.

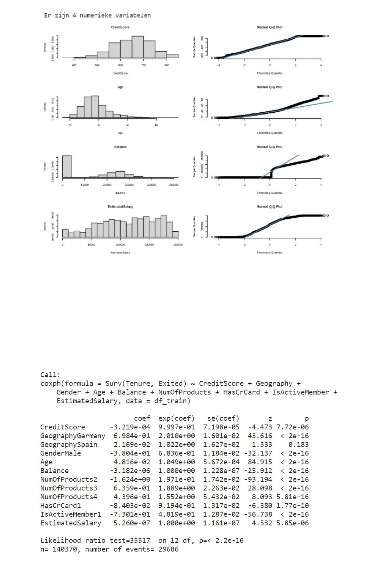
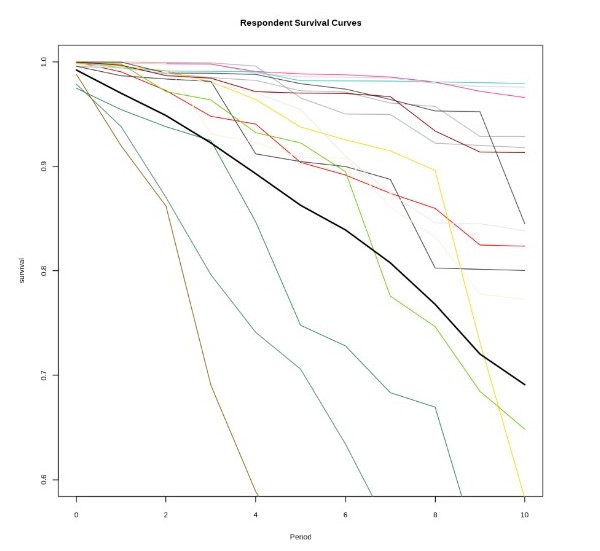
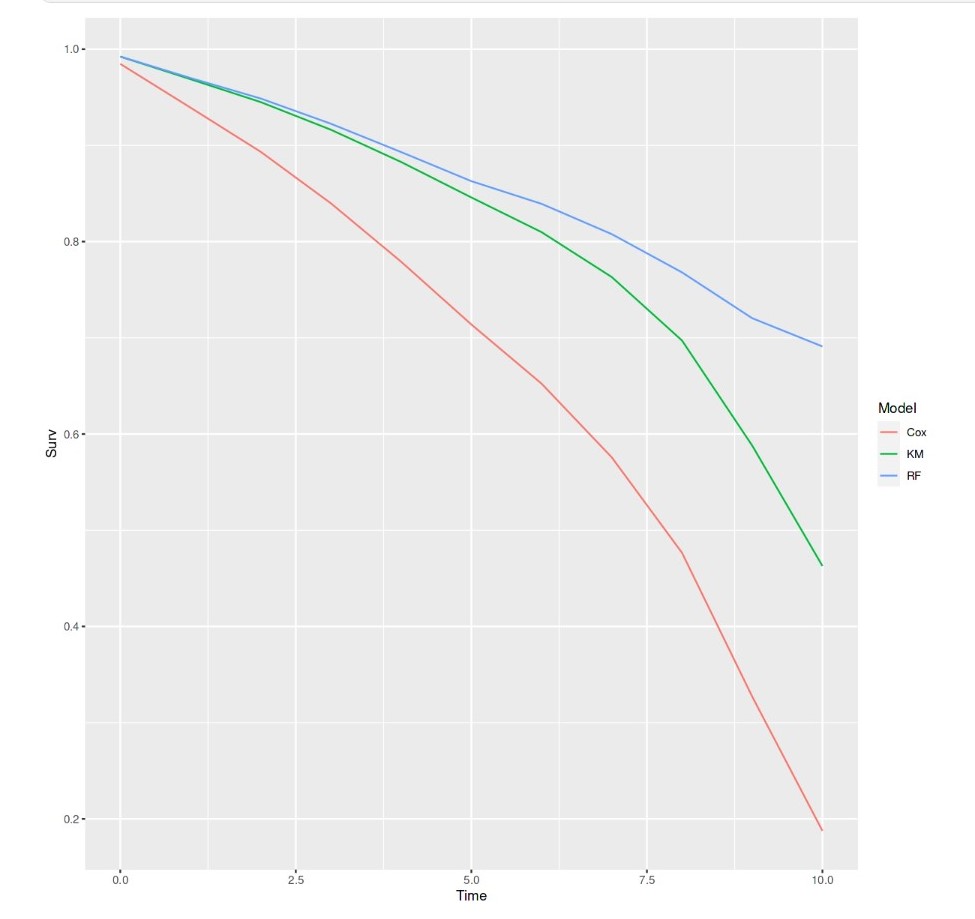
In dit artikel leggen we uit hoe we dit probleem kunnen aanpakken. Zo maken we gebruik van een analysetechniek die veel wordt gebruikt in medisch onderzoek, namelijk survivalanalyse. Ook zullen we laten zien hoe we te werk gaan aan de hand van een Kaggle Playground-case. Daarbij maken we gebruik van gegevens van de eerste competitie van 2024, gericht op het voorspellen van churn bij een bank. Deze dataset gebruiken we om de levensduur te bepalen met behulp van een Kaplan-Meier-plot, een Cox Hazard-model en een Random Forest-model. Voor onze oplossing hebben we gebruikgemaakt van R.

Essentie van Survivalanalyse

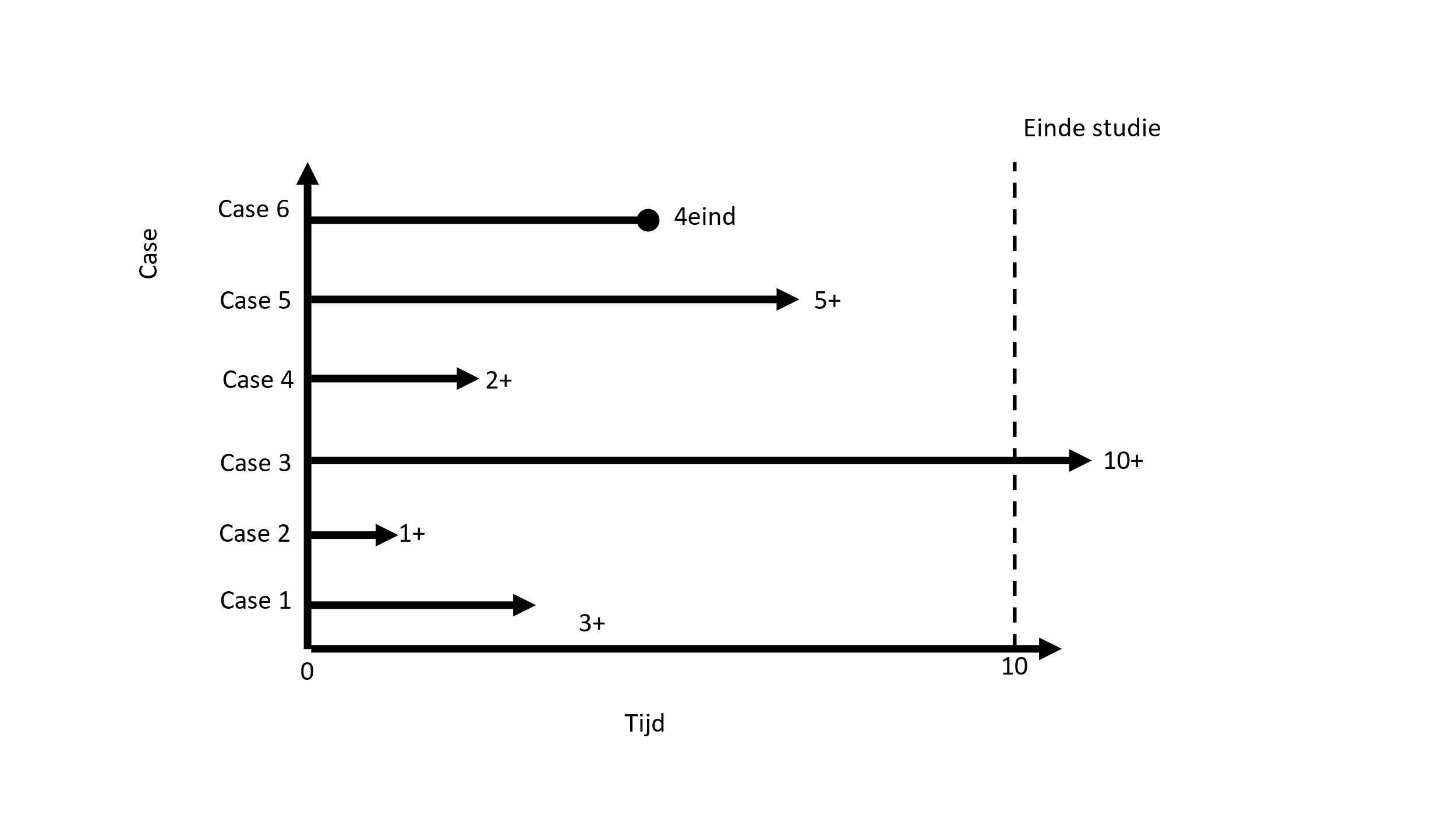
Survivalanalyse is een statistische methode die wordt gebruikt voor gegevens die informatie bevatten over de tijd tot het optreden van een bepaalde gebeurtenis, zie voorbeeld in het figuur hiernaast. Deze gebeurtenis kan variëren van overlijden tot terugval, herstel of een ander duidelijk gedefinieerd eindpunt. Het wordt vaak gebruikt in situaties waarin de tijd wordt gemeten in jaren, maanden of weken, vanaf het begin van de follow-up van een patiënt tot aan het optreden van de gebeurtenis. In een survivalanalyse wordt ervan uitgegaan dat er maar één type risico is en dat een gebeurtenis per individu hoogstens één keer kan optreden. Als er sprake is van meerdere risico’s of herhalingen van een gebeurtenis, zijn meer geavanceerde analysetechnieken nodig, zoals recurrent event-analyse of competing riskanalyse.

Een belangrijk concept bij het analyseren van tijd-tot-gebeurtenisgegevens is gecensureerde waarnemingen. Dit treedt op wanneer de volledige tijd tot het optreden van de gebeurtenis niet bekend is voor alle individuen in een studie. Dit kan gebeuren omdat de gebeurtenis nog niet heeft plaatsgevonden voor sommige individuen op het moment dat de studie eindigt, of omdat sommige individuen uit de studie verdwijnen voordat de gebeurtenis plaatsvindt.

Conclusie

Het bepalen van de levensverwachting of duur van een klant, abonnement of polis is een van de meest gestelde vragen aan een analist. Het berekenen hiervan op basis van de einddatum verminderd met de begindatum voor uitgestroomde klanten kan echter leiden tot een aanzienlijke vertekening, zoals ook bleek tijdens de uitwerking van deze case.

We hebben drie veelgebruikte methoden toegepast op de bankchurn dataset om de survival curve (en dus ook de duur) van de klant te bepalen. Dit zijn de Kaplan-Meier methode, Cox Hazard regressie en het Random Forest model. De uitkomsten van de verschillende methoden worden hieronder weergegeven.

Voor deze dataset blijkt dat het Random Forest model (8,5 jaar) de langste gemiddelde levensduur voorspelt, in vergelijking met de Kaplan-Meier curve (8,4 jaar) en de Cox regressie (7,2 jaar). Dit verschilt duidelijk van de naïeve bepaling van de duur (5 jaar).

Een voordeel van zowel de Cox regressie als het Random Forest model is dat op basis van deze analyses ook nieuwe cases kunnen worden geschat. In het geval van Kaplan-Meier ga je uit van het gemiddelde.

Deze modellen helpen marketeers om de levensduur van klanten nauwkeuriger te voorspellen, wat leidt tot effectievere klantbehoudstrategieën en gerichtere marketingcampagnes. Hierdoor kunnen middelen efficiënter worden ingezet en kan de klanttevredenheid en -loyaliteit worden verhoogd.

Ben je benieuwd naar de technische details van onze analyses of heb je vragen hierover? Laat het mij gerust weten of neem contact met ons op voor meer info!